 Сечение призмы
Сечение призмы
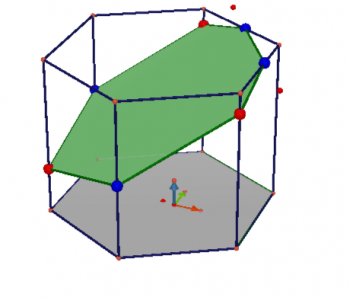
Пример 3. Призма с основанием правильным шестиугольником
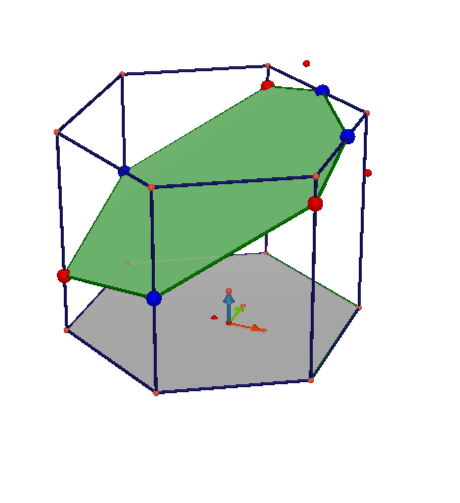
Строим сечение призмы по трём точкам, лежащим на рёбрах, но попарно не лежащих в одной плоскости. Используем параллельное проектирование
 Сечение призмы
Сечение призмы

Строим сечение призмы по трём точкам, лежащим на рёбрах, но попарно не лежащих в одной плоскости. Используем параллельное проектирование
 Сечение призмы
Сечение призмы
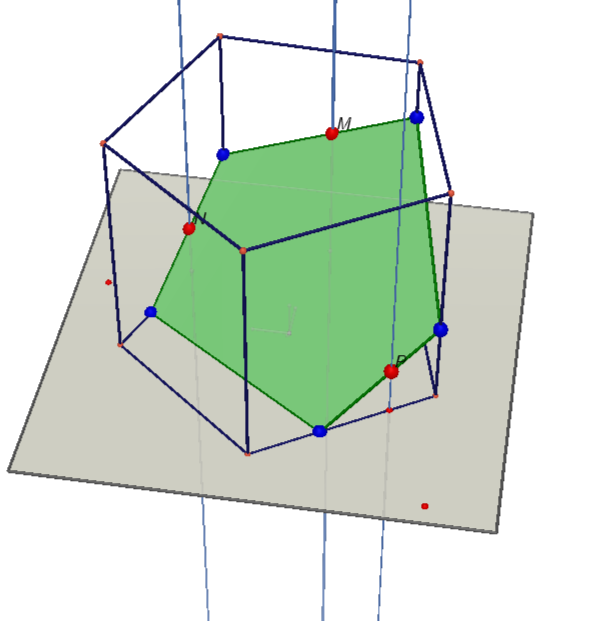
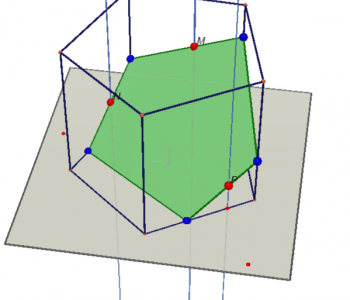
Более сложный случай, когда три точки не лежат на рёбрах призмы и не лежат попарно в одной плоскости. В этом случае необходимо использовать параллельное проектирование.
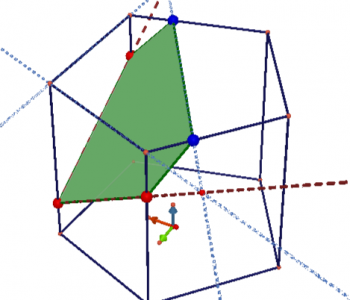 Сечение призмы
Сечение призмы
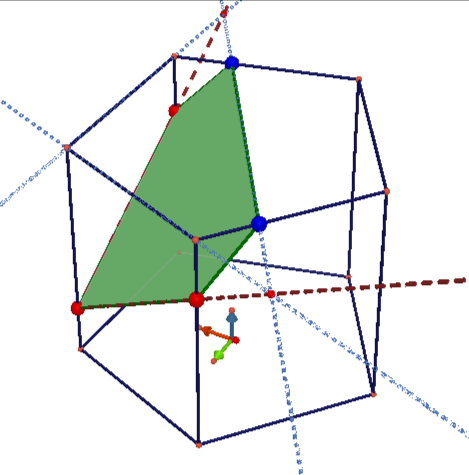
В основании прямоугольной призмы — правильный пятиугольник. По трём точкам, расположенным на соседних рёбрах, строим сечение.
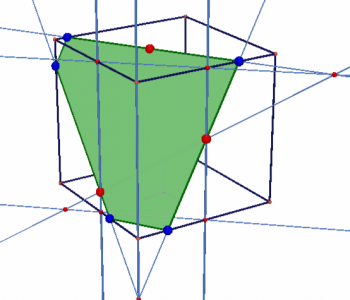 Сечение куба
Сечение куба
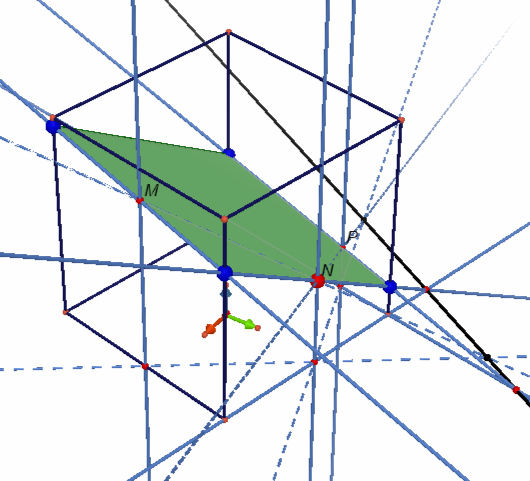
Более сложный случай, когда одна или две, или все три точки лежат не на рёбрах, а на гранях. Тогда используется метод параллельного проектирования, а именно: через эти точки проводим прямые параллельные какому-либо ребру, чтобы найти проекции этих точек на соответствующую грань. Например, проводим прямые, параллельные боковым ребрам и находим точки пересечения этих прямых с ребрами нижнего или верхнего основания.
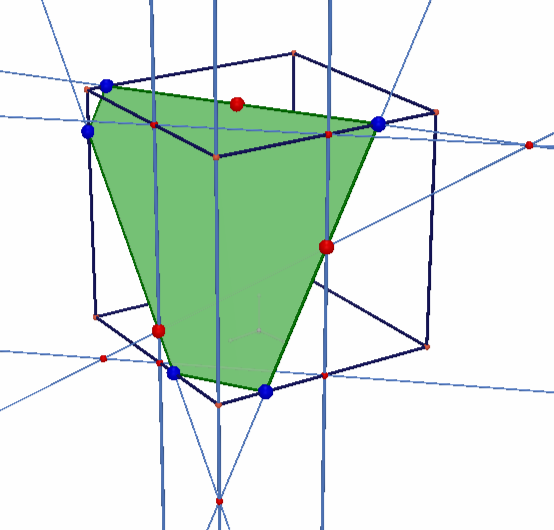
Ещё один пример применения параллельного проектирования.
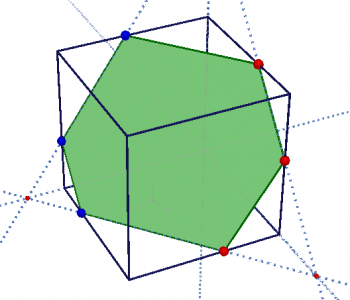 Сечение куба
Сечение куба
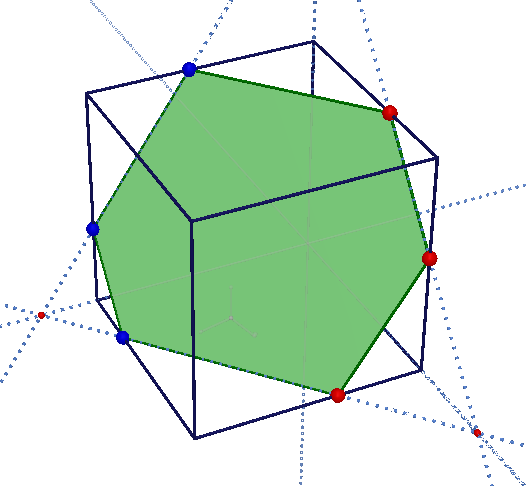
Довольно простое расположение трёх точек: попарно лежат в плоскостях граней. Но как видим, при определенном расположении в сечении появляется шестиугольник.
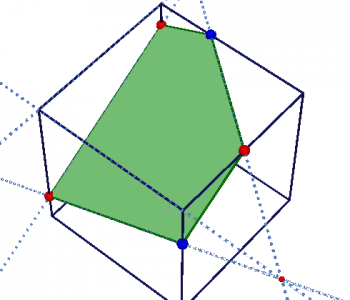 Сечение куба
Сечение куба
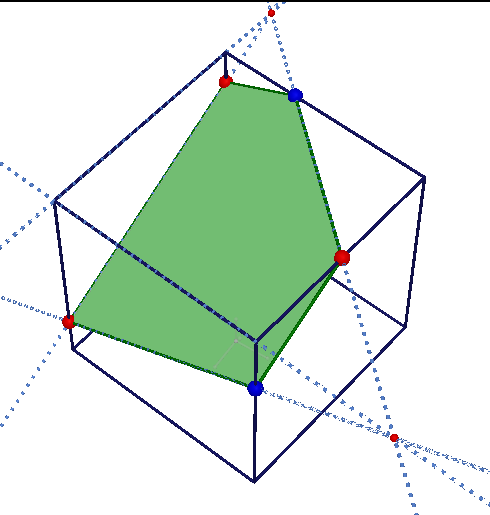
Здесь две точки находятся в одной плоскости левой боковой грани. Третья точка — на общем ребре верхнй и правой боковой граней. Как построить сечение? Один из вариантов смотри в видео…